Las propiedades mecánicas, entre todas las propiedades de los materiales plásticos, son con frecuencia las mas importantes, porque virtualmente todas las condiciones de servicio y la mayoría de las aplicaciones finales involucran algún grado de solicitación mecánica.

La selección del grado adecuado para una determinada aplicación se basa frecuentemente en la selección de propiedades mecánicas tales como Resistencia al Impacto, Rigidez y Resistencia a la Tracción. Los valores de cartilla de las propiedades mecánicas de los plásticos se generan a partir de ensayos realizados en un laboratorio bajo condiciones normalizadas, mientras que en las aplicaciones prácticas, los materiales no están sujetos a una deformación simple y continua, además de estar sometidos a factores ambientales adversos. Justamente a esto, se hace mención en la parte que se describe la relación de las propiedades mecánicas con la temperatura y la velocidad de deformación.

La comprensión básica del comportamiento de tensión-deformación de los materiales plásticos, es de suma importancia para comprender el significado físico de las propiedades mecánicas. A continuación se describe el diagrama de tensión-deformación graficado en la figura. Para una mejor interpretación de este tipo de diagrama, es preciso definir algunos términos que están asociados al mismo.

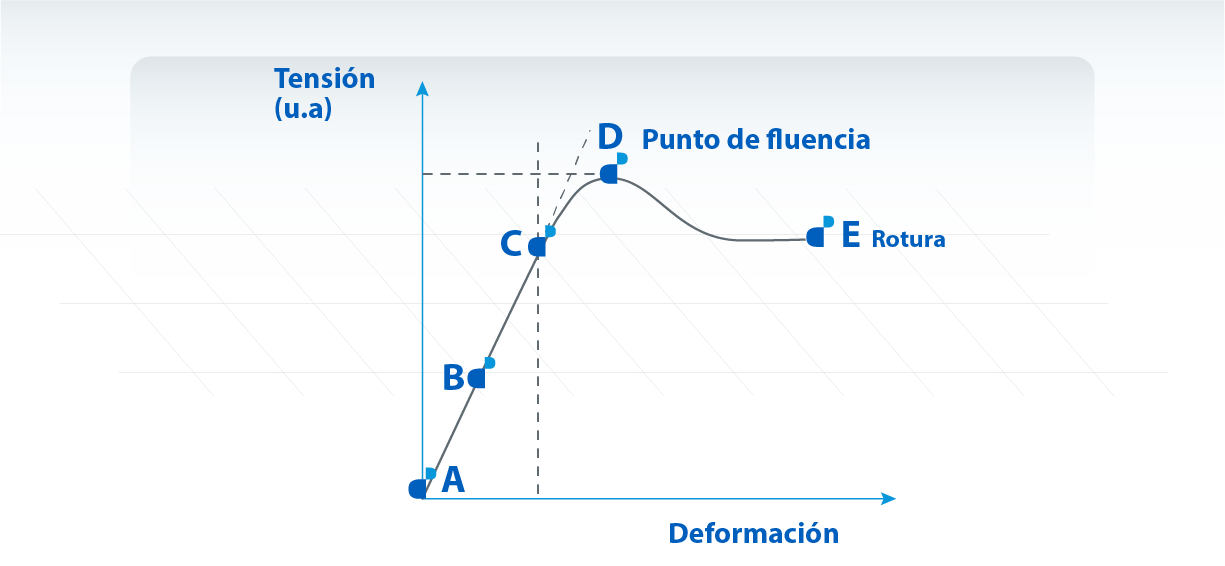
Diagrama de tensión-deformación

Definidos estos parámetros, profundizaremos el análisis del diagrama para analizar que tipo de información su puede extraer del mismo y como se relaciona esta información con las propiedades del material.

1. Módulo de Elasticidad en Flexión

Es una medida de la habilidad que tiene un material para soportar el pandeo cuando es sometido a una fuerza aplicada en forma perpendicular al eje longitudinal. El módulo de flexión se representa por la pendiente inicial de la curva tensión-deformación. Un valor alto de esta pendiente (alto módulo) implica que la pieza tiene una elevada rigidez.

2. Módulo de Elasticidad en Corte

El módulo de Corte es una medida de la dureza o de la resistencia que ofrece el material durante el proceso de torsión. Se mide precisamente en un péndulo de torsión, colocando una probeta rectangular y dándole un momento de inercia conocido calculando la amortización de la oscilación libre.

Al igual que el modulo de elasticidad en flexión es una medida de la rigidez de la pieza y se mide en fuerza por unidad de área.

3. Módulo de Elasticidad en Tracción

Es una medida de la resistencia que ofrece el material durante el proceso de elongación. Es un ensayo de gran importancia ya que a menudo los materiales en sus distintas aplicaciones se ven sometidos a esfuerzos de este tipo.

4. Resistencia al Impacto

Es una medida de la tenacidad del material, es decir la capacidad de la resina de absorber una determinada tensión sin romperse. La energía requerida para romper la muestra es la suma de las energías necesarias para deformar, iniciar y propagar la fractura y finalmente empujar los extremos remanentes.

En la gráfica tensión-deformación, la tenacidad se infiere a partir del área bajo la curva. Un material con mayor resistencia al impacto presentará una área mayor bajo la curva. Cabe aclarar que en los ensayos de resistencia al impacto la velocidad de deformación será sensiblemente superior a los ensayos de rigidez.

Métodos de ensayo de impacto

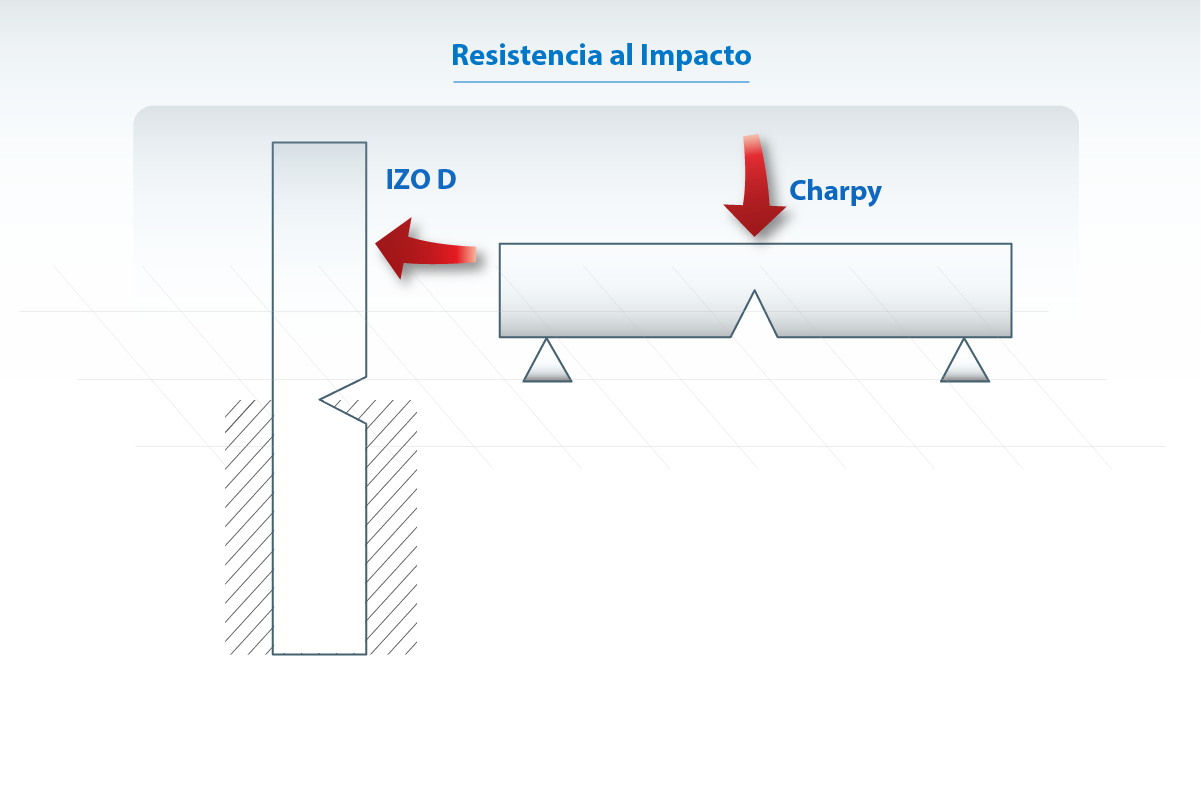
Generalmente se determina en forma práctica por dos métodos distintos la resistencia al impacto: IZOD y Charpy. En ambos casos, el objetivo del ensayo es medir el grado de resistencia de una probeta al golpe de un péndulo cargado con un determinado peso. El resultado se expresa en término de la energía cinética consumida por el péndulo para quebrar la muestra. La probeta puede tener entalla o no pero los valores obtenidos sobre muestras entalladas generalmente son mas precisos puesto que la fractura que se produce es del tipo frágil y no dúctil.

La diferencia entre IZOD y Charpy consiste en la ubicación de la muestra en el aparato. Mientras que para IZOD la probeta se ubica perpendicularmente y el péndulo golpea en un extremo, en Charpy la probeta se ubica horizontalmente y el péndulo golpea en la parte central de la misma.

5. Relación Propiedades Mecánicas-Temperatura-Velocidad de Deformación de corte

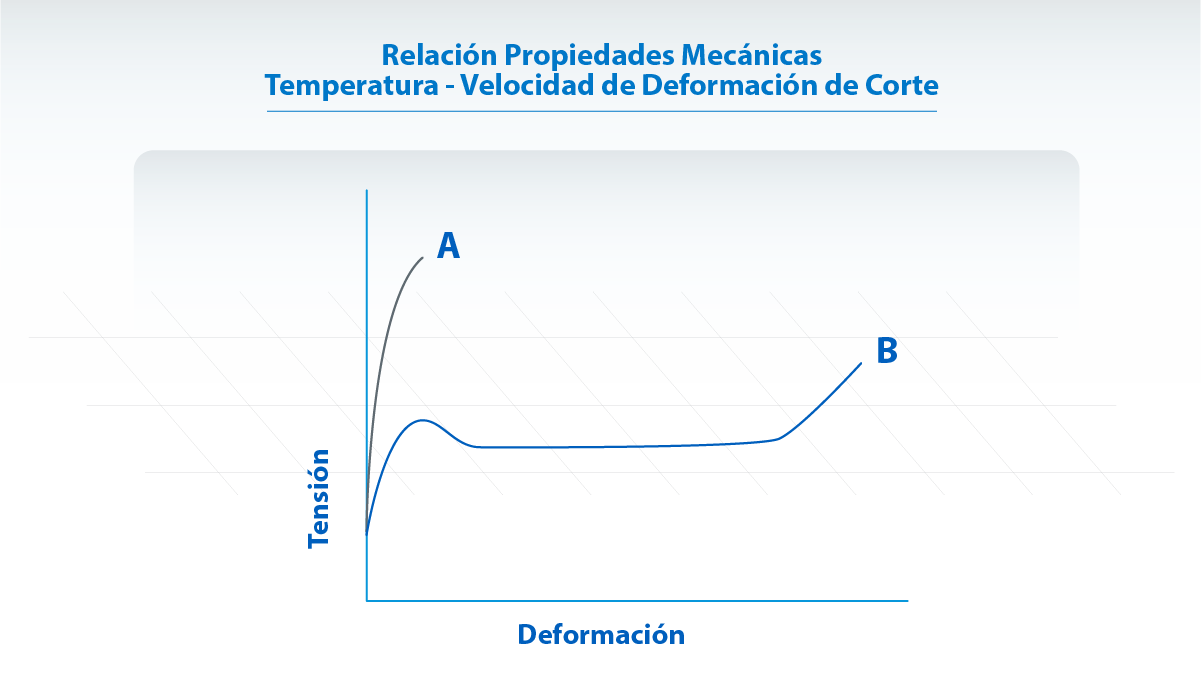
Hasta aquí analizamos las características de la curva de tensión-elongación de manera general. Cabe destacar que la forma de esta curva depende de manera marcada tanto de la velocidad con la que se aplica el esfuerzo como de la temperatura a la que se realiza el ensayo. Por debajo de una temperatura característica conocida como temperatura de transición vítrea, el material presenta una gran rigidez pero muy baja resistencia al impacto. Los materiales a esas condiciones de temperatura tienen los movimientos muy restringidos y la única forma de disipar energía es creando nuevas superficies por lo que se rompen a pequeñas tensiones aplicadas.

Comportamiento a diferentes temperaturas

Ese es el caso de la curva A de la figura. Este mismo material ensayado a una temperatura superior presentará un comportamiento del tipo de la curva B de la figura con mayor tenacidad (mayor área bajo la curva) y menor rigidez que la otra curva.

De manera análoga, de haber realizado el ensayo a temperatura constante pero a muy alta velocidad de deformación el comportamiento del material hubiera sido similar a la curva A de la figura y a una baja velocidad de deformación se hubiera parecido a la curva B de esa misma figura. Esta dependencia de las propiedades con las condiciones de determinación de las mismas deben ser consideradas al analizar la viabilidad de utilizar un determinado material para una determinada aplicación.

6. Propiedades de los Polipropilenos Cuyolen y Cuyotec

A menudo los materiales de alta rigidez presentan propiedades pobres de impacto mientras que los materiales tenaces poseen un módulo de flexión menor.

Los materiales Cuyolen y Cuyotec, presentan un buen balance entre estas dos características, que los hace apropiados en muchas aplicaciones. En la figura se representa la relación rigidez/tenacidad de los homopolímeros y copolímeros Cuyolen y Cuyotec.

Relación rigidez/tenacidad